

¿Valen Para Algo?
Corría el año 1.787. Un pequeño chaval de 10 años estaba en la escuela junto con sus compañeros. Tenía suerte, por esa época no a todos los chavales de 10 años de padres campesinos, ni siquiera una parte considerable de los mismos, se les permitían ir al colegio. Ya sea por el tan típico (y dañino) pragmatismo del corto plazo (¡eso no vale pa’na!), como por una necesidad real de contar con algo más de fuerza muscular para mejorar, aunque sea mínimamente, las posibilidades de alimentar una familia, el caso es que no era muy común entre los miembros de su clase social.
Ese día, el profesor, que no debía tener muchas ganas de chavalería, vaya usted a saber por qué, se enfadó. El gremio de los profesores ha conocido días mejores que los actuales en cuanto a respecto social y profesional se refiere, y el SXVIII era uno de ellos: se hacía sí o sí lo que le viniese en gana al profesor, estuviese o no fundamentado. El caso es que, para librarse de tanta muchachada, se le ocurrió un ejercicio estupendo: chicos, súmenme del 1 al 100, a ver cuánto sale. Qué buena idea, por dios, esto los mantendría callados durante una buena cantidad de tiempo. Debería tener más trucos como este, se dijo.
Pero, para colmo del profesor, un chaval levantó la mano a los pocos segundos asegurando tener la solución. El profesor, por supuesto, no le creyó, y le instó a que se dejase de tonterías y se enfrascase en el ejercicio, aumentando quizá un poco más su enfado. El chaval, insistió y obligó a que el profesor levantase el culo de la poltrona. Vio el resultado: 5.050. Bueno, pues un número como otro, al azar. El cuaderno no tenía los cálculos de suma de los 100 números, y es obvio que ninguna cabeza, por bien amueblada que esté, puede hacerlo sin ayuda y en tan corto espacio de tiempo. Por tanto, sin las 99 sumas, el número era sólo eso: un número. Las probabilidades de que el chaval hubiese acertado eran ínfimas.
Pero el chaval, insistió.
Y el profesor tuvo que comprobar su resultado. Se remangó, y tuvo que ponerse, él mismo, a hacer el ejercicio. Qué ironía, al final era él quien estaba cumpliendo su propio castigo…
Pero cuando acabó, el enfado se diluyó dando paso a un enorme asombro: ¡el resultado era correcto! ¿Cómo era posible?
Se acercó, revisó los poquísimos cálculos del chaval, y le preguntó acerca de método. El chaval, con todo convencimiento, expuso su idea: en lugar de sumar los 100 números, sumó sólo el primero y el último, de forma que observó que 100 + 1 = 101. Luego sumó el penúltimo y el segundo, y vio que 99 + 2 = 101. Sumó el antepenúltimo y el tercero, y obtuvo de nuevo que 101 = 98 + 3. Era suficiente. Si emparejaba los números de la lista dos a dos por sus posiciones simétricas, siempre obtenía 101. ¿Cuántos pares posibles hay en 100 elementos? 50. Pues hecho: 101 x 50 = 5.050. Tenía que ser correcto, no había otra opción. Su razonamiento era válido.
No os costará creer que al profesor se le cayeron los pantalones.
Pues bien, este chaval, que no era otro que Carl Friedrich Gauss, acababa de descubrir, a sus 10 añitos, la fórmula de la suma de una progresión aritmética. Por supuesto, se convirtió en (o más bien, ya era uno) de los mayores matemáticos de la historia.
La fórmula quedó tal que así1:
Y tiene una aplicación muy sencilla: supongamos el caso de la suma de los 100 primeros números naturales, tal cual propuso el profesor de
Gauss. En ese caso, el truco es sencillamente saber que n=100, y que a1 se refiere siempre al primer elemento de la serie, y an, al último. De esta forma con unas sencillas sustituciones de los términos por sus correspondientes valores, obtenemos de inmediato que
Como veis, las matemáticas no son fórmulas a aprender, sino que son pensamiento formulado. Esta fórmula superior es, sencillamente, la forma de escribir el razonamiento mental de Gauss, que consistía en sumar el primer y último término (1 + 100 = 101), y multiplicarlo por el número de parejas que podía hacer (100 / 2 = 50). Fin.
Las fórmulas no existen por que sí, ni son fruto de un azar técnico o un capricho matemático, sino que son un razonamiento encapsulado. Enlatado. Son lógicas, coherentes, y sencillas. Aplicando la secuencia de pasos adecuada, todos llegamos a la misma conclusión sencillamente aplicando nuestra capacidad de razonamiento lógico.
Espera, espera, listillo. ¿Estás insinuando que todos nosotros somos genios de las matemáticas? Que yo las vengo pasando raspadas toda la vida, y nunca he entendido ni papa. Y tampoco creo yo que tú seas una eminencia…
_____________________
1 No es la variante más generalista y utilizada.
¡Hombre, hola! Me alegro de que estéis por aquí. Con un tema tan espinoso, no esperaba mucha asistencia, la verdad.
No, no quiero decir, ni de lejos, que todos seamos unos genios de las matemáticas. Ni que vosotros no, pero yo sí. Para nada.
Quiero decir que, una vez alguien ha identificado, gracias a sus capacidades de razonamiento, algo nuevo, si nos hace caminar por sus mismas secuencias de pensamiento, llevándonos por supuesto de la mano, acabaremos redescubriendo por nosotros mismos lo que esta persona ya descubrió primero.
Y ahí está la clave: el genio es quien es capaz de, partiendo de la inexistencia de un razonamiento, tomar otros, juntarlos, razonar por sí mismo sin ir de la mano de nadie, y generar nuevo conocimiento. Los que luego, a posteriori, sólo somos capaces de andar el camino ya por él generado, somos simples mortales.
Pero el camino lo podemos recorrer sin mayores problemas, siempre que nos lo muestren. No es tan complicado.2.
Esto es muy similar a lo que ocurre con el arte, por no decir que es exactamente lo mismo: que no seamos capaces de concebir una gran obra musical, de plasmar realidades y fantasías en un cuadro, o de imaginar historias y mundos paralelos y escribirlos en un libro, no nos resta ni un ápice de posibilidades de disfrutarlos.
El genio, los crea, pero el mortal puede, sin límite, comprenderlos y disfrutarlos. Las matemáticas también entran en esa horma.
No, no, no, y rotundamente no. Por esta sí que no paso. Llevo toda mi vida disfrutando de la música, la pintura, y la literatura, y jamás he creado nada. Pero las matemáticas no las he comprendido en la vida, ni mucho menos disfrutado. No me está gustando esto que estás liando.
Estoy de acuerdo con vosotros. Esto también es cierto, pero hay que buscar otros culpables externos a las propias matemáticas en sí. El problema es otro. El problema es cómo nos las enseñan.
Si a vosotros, como a mí, en la EGB, creo que en séptimo, os enseñaron la fórmula de arriba con el bonito titular de suma de una progresión geométrica de n elementos, pues mire usted, le quitan todo el glamour. Si a esto añades que te dan otras diez o doce fórmulas más para que te aprendas, y luego te examines, obviamente uno va, poco a poco y sin darse cuenta, apartando las matemáticas al rincón de las cosas feas, y las deja allí encerradas, al lado de otras como madrugar o pasar hambre. Y entra en ese rincón sólo cuando no le queda más remedio.
_____________________
2 Por supuesto, realizar ciertos razonamientos implica tener ya cierto conocimiento previo de partida, base para los mismos. Es decir, si bien seguro que podemos recorrer cualquier camino, es posible que, para hacerlo, debamos primero recorrer otros para adquirir una experiencia previa en el viaje, y ser capaces entonces de comprender lo que vemos. Pero esto no cambia la esencia del argumento, sencillamente lo simplifica para que la discusión pueda continuar con fluidez.
Ya, vale, entiendo por donde vas. Pero no pueden contarnos una historia motivadora para cada fórmula a ver si nos llama la atención, y ver si así la razonamos y la interiorizamos. No daría tiempo a casi nada.
Mmmmmmm, permitidme que discrepe. Estoy de acuerdo en que no te pueden estar contando historias para cada fórmula. Esto es una visión demasiado romántica acerca de los métodos de enseñanza, lo reconozco. Pero es que no es necesario. Me explico.
Si en lugar de soltarte una fórmula y mandarte 15 ejercicios que luego hay que corregir, te explican su concepto, aquello que representa, es muy probable que lo entiendas. Si lo entiendes, ocurrirán dos cosas: la primera, es que no necesitarás saberte la fórmula. Podrás razonarla cada vez que la necesites. Y esta sensación es bonita, transmite control e inteligencia, lo que hace que, poco a poco, vayas retirando las matemáticas del rincón de las cosas feas, y las vayas acercando al de las cosas divertidas.
Os garantizo que la fórmula que hemos utilizado en el ejemplo anterior no la he tomado de ningún lugar, de ahí que no haya referencia a la fuente, sino que la he deducido de cero, expresamente para escribir este artículo, ya que conocía el razonamiento que hizo Gauss. Esto no la convierte en mía, por supuesto, ni me otorga ni un gramo de la inteligencia ni el ingenio de Gauss. Tan sólo, me sirvo de ellos.
Y esto es infinitamente más gratificante que tener que llevarla grabada en la mente, o tener que ir a buscarla a un libro. Esto, me divierte.
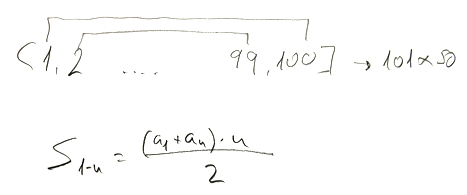
Y la segunda cosa, es una derivada de la primera, pero lo suficientemente importante como para que tenga entidad propia: el concepto es mucho más amplio que la técnica. Un mismo concepto tiene, casi siempre, una gran multitud de fórmulas asociadas en función de los distintos ámbitos, contextos, y medios en los que éste se aplique. Si se conoce el escenario concreto, se pueden extraer de este las aplicaciones particulares. Pero lo contrario es mucho más difícil, y sí está circunscrito a mentes con capacidades y/o entrenamientos superiores a la media. Deducir es más fácil que inducir.
Por tanto, una misma historia, ahorra varias fórmulas, varios paquetes de ejercicios, y varios paquetes de corrección de ejercicios. Visto así, no lleva más tiempo, es más divertido, y motiva. Es mejor.
Pero para esto, nuestros educadores deberían ya haber sido educados en el concepto y no en la técnica. Si el educador no tiene la esencia, es imposible que se la transmita al chaval. Pero bueno, este tema es garbanzo de otro cocido que no toca cocinar hoy.
Bueno, ¿cómo vamos? ¿Qué os está pareciendo? Es un tema espinoso, lo sé, me interesa mucho vuestra opinión…
Bueno, no va mal. Pero hay miedo. ¿no te irás a flipar con los números y los símbolos y nos meterás una chapa, verdad? Dinos qué pretendes, porfa, no vaya a ser que haya que irnos, y si es así, cuanto antes, mejor.
Bien, me parece justo. Hoy no vamos a hablar de matemáticas. Hoy vamos a hablar de para qué sirven las matemáticas. Qué podemos obtener de ellas. De por qué debemos no sólo no desterrarlas de nuestros intereses, sino de porqué debemos prestarle más atención a nuestra formación y recursos matemáticos.
Vale, gracias por todo. ¡Adiós!
¡Esperad, esperad!
Que no, que no… Que ya me han intentado convencer de esto más veces. Como dice Robe en Extremoduro: “me voy que to cosas cacer…”

¿Qué haces? ¿Soltando bombas a traición?
Lo siento. No es mi estilo, pero no me habéis dejado otra opción. Os veo un poco tercos con este tema, y creo que salir corriendo os hará estar ciegos ante realidades (sí, sí, realidades) que no podemos obviar.
Y esta realidad, contrastada, y es importante esta palabra, es que, cada vez más, en los trabajos se requiere formación matemática. Y que los ascensos y puestos más relevantes están cubiertos por personas cuya relación con las matemáticas puede ser mejor o peor, pero, desde luego, no es ni de miedo, ni de rechazo. Las afrontan de cara.
Es decir, amig@s, os guste o no, las matemáticas son viruta. Se traducen en dinero. Y con el dinero, se paga la cerveza. Y esto es serio, muy serio, ya que puede que no tod@s queráis cerveza3, pero seguro que tod@s queréis dinero.
Hay decenas de estudios, de distintos ámbitos, enfoques, y disciplinas, que dejan esto claro. Si os vais hoy, estaréis renunciando a una serie de oportunidades económicas. No porque aquí vayamos a aprender a ganar dinero, para eso debería haberlo aprendido yo primero, cosa que no ha ocurrido, sino porque, quizá, podamos poner en revisión nuestra relación con las matemáticas, y obtener un beneficio de ello.
No digo cambiarla, digo revisarla. Luego, igual la dejamos como estaba, pero es una oportunidad que creo que debemos darnos.
Vale. Me quedo. Pero soy asistente de enfermería, a ver cómo me convences de que en mi trabajo, las matemáticas me van a servir de algo... ¡Suerte!
Bien, entiendo. Y acepto el reto. Para empezar, no vamos a hablar sobre tu profesión, sino de cómo encaras tu profesión.
Vaya, buen regate… Pero esto no deja de ser un truco. Me voy.
No, hombre, danos una oportunidad, por favor, que estamos pocos. Déjanos intentarlo, ¿de acuerdo?
Vale. A ver de qué eres capaz.
¡Gracias!
En nuestros trabajos, en unas u otras proporciones, se nos requieren básicamente 2 cosas: esfuerzo y pericia muscular (sacar escombros, teclear código, llevar cubos de uva a la upa, hacer una factura, soldar una tubería, etc.), y una toma de decisiones prácticas (elegir las herramientas y el itinerario adecuados, analizar y diseñar previamente los procesos, saber la forma más óptima y de menos esfuerzo de llevar y repartir el máximo de cubos y no dejar a nadie esperando, diseñar previamente el recorrido concreto de la tubería y elegir correctamente los mejores puntos de unión, y saber soldar, etc.)
Y el esfuerzo, dependerá de la estrategia. Es decir, una mala estrategia de recogida y reparto de cubos puede que haga que, como cubero, me esté moviendo más que los precios, trabajando como una mula, pero tenga a media cuadrilla esperando cubo cada dos por tres. Poner otro cubero solucionará seguro el problema, claro. Pero puede que, si revisamos la estrategia, sólo con uno trabajando de forma más ordenada, consigamos el mismo resultado. Y con menos dinero. AHÍ está la clave.
_____________________
3 Por algún extraño motivo que no alcanzo a comprender, pero que, por supuesto, respeto.
Más allá de que la forma óptima de recorrido que maximice el reparto y recogida de cubos es un problema matemático de libro (y no de los obvios, por cierto, básicamente por lo dinámico del entorno), no vamos, como he dicho antes, a centrarnos en un trabajo concreto, sino en los enfoques generales. Y usaremos algunos ejemplos para que esta disertación, a caballo entre el ensayo y la filosofía aplicada, sea más amena y nos sirva como base empírica de que, efectivamente, el pensamiento matemático puede aportar, y de hecho lleva haciéndolo durante toda la historia, un valor tangible y concreto a nuestros trabajos. Eso lo saben los que pagan 4, y de ahí que lo valoren.
A ver, a ver, que me pierdo. ¿Me estás diciendo que, para mejorar mi trabajo como cubero tengo que coger papel y lápiz, apoyarme en el pescante del remolque, y ponerme a hacer cálculos de los que no tengo ni idea? ¿No crees que es así como justamente me despedirían? ¿Tú has sido cubero alguna vez?
No, sí, y sí, respectivamente
Como he dicho antes, no se trata de acciones concretas en el trabajo, sino de usar el pensamiento matemático en el trabajo. Veamos un ejemplo.
Si cuando estás de cubero, en lugar de, sencillamente, intentar correr todo lo que puedas, cogiendo cubos de dos en dos en cada mano en los momentos en los que se te aburrulle la harina, y siguiendo las voces de ¡cubo!, estableces una estrategia, trabajarás menos y mejor. Eso que se lleva tu cuerpo, y eso que se lleva el bolsillo del amo. Para que gane uno, no tiene porqué perder el otro.
Si en lugar de hilos, ves una matriz de NxM, compuesta por las cepas de los hilos que en ese momento estén siendo vendimiados, llamémosla matriz viña, y si en lugar de personas vendimiando, ves un grafo compuesto por cada una de estas personas, llamémoslo grafo personas, cuyos nodos quedan unidos por los posibles caminos entre cepas de la matriz viñas, seguro que, con sólo eso, y la intención de
maximizar las entregas y recogidas de cubos minimizando carga y recorrido, mejorarás tu forma de trabajo5. Sin lápiz ni papel. Sin cálculos previos. Esta forma de abordar el trabajo se basa en un enfoque matemático, pero no requiere de ningún trabajo matemático. Basta con, en cada viaje, intentar encontrar el mejor camino. Tu capacidad de razonamiento, y la experiencia que vayas acumulando fruto de realizar los miles de viajes que vas a hacer en un solo día, harán el resto por ti. Y de paso, mantienes la mente entretenida.
Tampoco es que estés buscando una solución óptima, tan sólo necesitas una que mejore tu forma de trabajo actual sin aplicar un pensamiento matemático. Con simplemente eso, ya te cansas menos, rindes más, y te entretienes.
_____________________
4 Bueno, es cierto, no todos lo saben. Algunos.
5 Este es tan solo un enfoque, el primero que me ha venido a la cabeza. Hay más aproximaciones para abordar este problema, pero esta, por su sencillez e intuitividad es la que yo he usado cuando he tenido que hacerlo. Sí, he llegado a ponerla en práctica, tengo problemas mentales, lo sé.
Ya vamos cogiéndole el gusto a esto de las matemáticas, va a resultar que sí valen para algo…
Para. No sé lo que son esas cosas que dices. Y no pienso abrir un libro antes de irme a las viñas, por ahí sí que no paso. No quise estudiar entonces, voy a hacerlo ahora, ¡¡pues sí hombre!!
Lo entiendo, y lo comparto. Y no lo necesitas. Yo los he llamado por sus nombres técnicos, pero como hablamos de imaginar, ni siquiera los necesitas.
Una matriz es una tabla con elementos. Si has cortado hilos de 10 cepas, y en un momento dado tienes 7 vendimiadores, tienes una matriz 10x7.
Un grafo son puntos que están unidos por caminos. Tu grafo es de 7 puntos, uno por persona. Siempre usarás el camino más corto entre 2 puntos, por intuición. Obviamente, entre dos vendimiadores con cubos llenos que están al lado, en cepas contiguas (lo que se denomina, en teoría de grafos, distancia 1), no le recogerás el cubo a uno, te irás a la casa a por espuertas, y a la vuelta se lo cogerás al de al lado. Sin pensarlo, retirarás los dos en la misma vuelta, eso ya lo llevas puesto de serie.
Llámalos por tanto como quieras, intuitivamente no necesitas un nombre para ellos. Basta con que los estructures mentalmente.
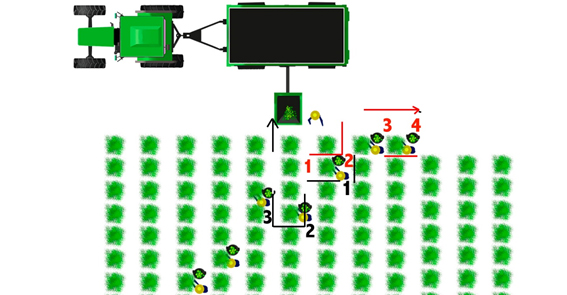
En definitiva, se trata de pensamiento estructurado. Y esto aporta valor sea cual sea tu profesión. Y por eso se paga.
Bien, bien, te veo suelto hoy. Tienes razón, tener la cabeza bien organizada, es algo que efectivamente es positivo, pero eso ya lo sabíamos, y para ello no necesitamos las matemáticas. Si sólo querías contar esto, te has ido a Cádiz por Zamora 6, siento decirlo.
Una vez más, sí, y no. Si ya tienes una cabeza organizada, enhorabuena. En ese caso, efectivamente, para ti todo esto es simple intuición. Te sale solo.
Pero la mayoría de los mortales necesitamos, primero, entrenar, y luego, disfrutar de los resultados. Si eres de ese tipo de personas a las que les cuesta estructurar los problemas y romperlos en trozos más pequeños, la mejor forma de enseñar a la mente a esto es usar el pensamiento matemático. Forzarse a hacerlo. Como todo, al principio, no es sencillo, pero tras unos pocos intentos, os garantizo, que el poder de las matemáticas, aunque no las estéis aplicando directamente, os regalará unas secuencias de pensamiento más estructuradas, las cuales tenderéis a aplicar sin saber que, al hacerlo, estáis siendo matemáticos. Como le pasó a Gauss de chaval: sencillamente razonó. La fórmula, la pusieron los mayores. Pero es suya.
Bien, sigamos. Como bien decís, vamos a ver otras ventajas que podemos obtener de las matemáticas, pero que no requieran que se estudien matemáticas. Vamos a ver más formas de aprovecharnos de las matemáticas, que bastantes disgustos nos han dado ya.
Vamos a hablar de tres grandes aportes que podemos, con sencillez, obtener: vamos a aprovechar su capacidad de deducción, su capacidad de predicción, y su capacidad de abstracción.
Sobre la primera vamos a discutir, ya os lo adelanto, así que vamos al lío. Sin rencores, ¿vale?
Siento decirte que te equivocas con frecuencia. Con mucha más frecuencia de lo que eres capaz de reconocer, pero, y lo que es peor, con mucha más frecuencia de lo que eres capaz de identificar. Y yo. Y ella. Todos y todas.
Venga, no te vengas arriba. Todos metemos la pata, pero no tanto.
Siento estar en desacuerdo. Tanto. Y más. Y el problema es que, como decía Bunbury, “los sentidos me distraen, y se equivocan”. Y no hace falta alcanzar el nivel de narcóticos al que veladamente hace referencia la canción. Es, lamentablemente, una norma. Una carencia intrínseca de nuestros cerebros.
Nuestra capacidad de razonamiento y nuestra intuición son, a menudo, difíciles de separar. Nuestra mente lógica suele llevar razón. Pero menos veces de las debidas le preguntamos, dado que, nuestra mente intuitiva, de respuesta más rápida, pero también más impetuosa y orgullosa, nos contesta antes. Y nosotros, ingenuos, tomamos esta respuesta como válida, y nos generamos ejemplos lógicos que la justifican.
_____________________
6 Desde Tomelloso, se entiende.
Es decir, no seguimos la secuencia correcta de un razonamiento lógico: primero analizar la situación, y luego alcanzar una conclusión, sino que, con la conclusión ya en la mano, generamos las situaciones que la justifican. Esto se llama sesgo de confirmación, y nos pasa a todos constantemente.

Aristóteles, que no era precisamente tonto, razonó un día que, si soltaba a la misma altura un martillo y una pluma, el martillo tocaría antes el suelo. Al fin y al cabo, si coges un martillo y una pluma, y los sueltas a la misma altura, el martillo toca antes el suelo que la pluma. Esto le llevó a afirmar que los objetos más pesados caen al suelo con mayor rapidez. Y si lo pruebas, obtienes lo que predice Aristóteles, así que tienes que darle la razón. Y al hacerlo, curiosamente, ambos estaréis equivocados.
A Galileo, siglos después, algo le olía mal. No vamos a entrar en los motivos. El caso es que, el hombre, haciendo sus fórmulas por aquí para unas cosas, y por allí para otras, obtenía una conclusión diferente. Según sus cálculos, basados en las matemáticas, ambos objetos deberían caer a la misma velocidad, ya que la velocidad a la que lo hacen no depende de sus masas, sino que depende únicamente de la masa de la Tierra, la cual es la misma para el martillo que para la pluma 7. Galileo decía que ambos cuerpos, martillo y pluma, deberían caer acelerando a unos 10m/s, independientemente de su masa, y, por tanto, tocar el suelo a la vez.
_____________________
7 Esto tiene sus peros, ya que era, también, una observación parcial. Eso sí, mucho más precisa y generalista, no sujeta a las condiciones del entorno. Realmente la Tierra no atrae a la pluma ni al martillo. El sistema martillo-pluma-Tierra genera una interacción gravitatoria mutua que acaba generando un centro de masas común y externo a los centros de gravedad individuales de cada uno, hacia el cual, los tres cuerpos se ven atraídos. Es decir, la pluma también atrae no sólo al martillo, sino a la Tierra. Es la enorme disparidad de masas Tierra-[pluma-martillo], y la casi idéntica entre la pluma y el martillo (en el sistema de referencia mencionado), la que hacen que pluma y martillo se comporten igual entre sí, y sustancialmente diferente a la Tierra. Pero atraerla, la atraen.
De nuevo, nuestros sentidos se equivocan. El Universo no funciona así, aunque seamos incapaces de apreciarlo. Lo que percibimos no es lo que ocurre.
Y efectivamente, hoy sabemos sin lugar a duda que pluma y martillo caen acelerando al mismo ritmo, de 9,81 m/s, y que, por tanto, tocan el suelo al mismo tiempo. No depende de sus masas.
Lo que sí depende de sus masas es la resistencia que oponen al aire. Por tanto, el aire sí frena mucho más a la pluma, por tener esta menos masa que el martillo, y poder por tanto contrarrestar menos el rozamiento, el cual afecta mucho menos al martillo, y, por tanto, cae más rápido, alcanzando antes el suelo.

Galileo, aparte de otros grandes aportes, fue uno de los primeros en saber que, para alcanzar conocimiento razonado y debidamente justificado, la intuición no era el mejor vehículo. Y que las matemáticas, cuando estaban bien hechas, parecían, casi mágicamente, arrojar siempre las respuestas adecuadas. Por poco intuitivas y contrarias a la experiencia que fuesen estas respuestas, cuando se ponían a prueba, siempre acababan siendo válidas, y, tras estudiarlas, se acababa comprendiendo el error en el que había caído nuestra intuición. En este caso, nuestra intuición había obviado el rozamiento del aire, quizá porque no sentimos que estamos inmersos en un océano de gas, sino que sentimos que estamos libres sobre el suelo. Al obviarlo para una cosa, lo acabamos obviando para el resto.
Luego llegó Newton, con su empirismo matemático absoluto, y revolucionó la ciencia. Se pasó por el arco del triunfo su intuición, y se embarcó en un viaje con dos únicos compañeros: las pruebas, y las matemáticas. Y se convirtió en el mayor científico que la humanidad haya tenido 8.
Las matemáticas tienen, por tanto, un poder de inducción y deducción del que nuestra intuición carece. Aceptarlo o no, no es cuestión de preferencias, es, sencillamente, cuestión de orgullo.
_____________________
8 Y tuvo sus autenticas barbaridades y aberraciones que quiso hacer pasar por ciencia. Pero su pasada de frenada no debe nublar, ni un poco, sus increíbles aportes. Así que a callar se ha dicho.
No es necesario poner un ejemplo de cómo esto te puede venir bien en el trabajo. Que se lo digan a un calderero, a ver si para prever la presión que aguanta una cisterna es mejor sacar el dedo al viento, o hacer algún calculejo, aunque sólo sea para asegurarse.
Sobre la capacidad de predicción de las matemáticas no vamos a discutir. Ni nos vamos a ir a siglos pretéritos buscando lumbreras. Nos vamos a quedar aquí, ahora, y entre nosotros.
Seguro que alguno de vosotros, apostáis. Aquí uso vosotros no en su vertiente inclusiva, sino masculina. Por desgracia, caemos mucho más en esta engañifa que ellas. Luego queremos ser tod@s iguales, y no puede ser…
Bien, si lo hacéis, espero que poco. ¿Qué por qué? Porque fijo que perdéis. Y lo sabéis.
¡¡Eh, tú, que yo sé de fútbol, y gano muchas veces!!
A otro perro con ese hueso. No dudo de tus conocimientos futboleros, pero si sumas lo apostado y lo ganado, sales perdiendo. Te apuesto lo que quieras.
Y si no, aparte de pagarte mi apuesta (esto me pasa por apostar), para ahora, es el momento. Si sigues, vuelvo a hacerte la misma apuesta en unas semanas, que quiero recuperar mi viruta.
No, en serio, para. No hay peor cosa que juntar estadística y sentido común. Veamos.
Todos sabemos que, al lanzar una moneda al aire, el 50% de las veces saldrá cara, y el 50%, saldrá cruz. Hasta ahí, bien, todos de acuerdo.
Pues te planteo el siguiente negocio: tráeme a 100 amigos. No muy amigos, que dejarán de serlo. Con conocidos, me basta. Mejor, tráeme a 100 personas que te caigan mal. Y no, tú no puedes jugar, que ya vas viendo de qué va esto…
Yo tiraré una moneda al aire. Está prohibido apostar hasta que, por casualidad, haya salido cara 3 veces seguidas.
Todos apostamos 50€. A quien apueste lo contrario que yo, si gano, le recojo el dinero, y si pierdo le dejo que lo retire y le entrego 50€ adicionales. A quien apueste lo que yo, si ganamos puede recoger sus 50€ y yo les entrego otros 50, y si perdemos, perdemos nuestro dinero. Un clásico, vamos.
Cuando salen 3 caras seguidas, abro la mesa.
Los estudios, que los hay a patadas, indican que la mayoría de las personas verán más probable que salga cruz, porque ya toca más. Por tanto, en el peor de los casos, y siempre según los estudios, al menos una persona más apostará por cruz de las que lo harán por cara. Yo elegiré cara, claro. A la m1€rd@ la intuición, que la mía nunca ha sido buena.
De esta forma, con los que apostaron por cruz, tendré el dinero necesario como para devolver el dinero de los que apostaron por cara, y aún me sobrará uno: mis 50 €. Todos los cara hemos ganado 50€. Cuanta más gente apueste cruz, más dinero gano yo, y voy ganando amigos, porque, además, reparto ganancias. Genero motivación por el juego completamente gratis. No lo pago yo.
Dado que esto es una tendencia, cuantas más veces la repita, y cuanta más gente participe, más ganancias me aseguro. Perderé algunas rondas, seguro, pero las ganancias compensarán las pérdidas en la proporción que predicen los estudios. Hasta que la gente se de cuenta. Es decir, hasta que pongan por encima de su intuición, su capacidad de razonamiento.
Sin embargo, una breve lectura, de minutos, a la teoría de la probabilidad, les hubiese permitido saber qué es una variable independiente, y que cuando tratamos estadísticamente con éstas, la probabilidad de cada nuevo evento no está influenciada por el resto. Es decir, las tiradas anteriores no afectan en absolutamente nada al resultado de la tirada actual. No dependen de ellas. Siempre hay un 50% de probabilidades de que salga cruz, con independencia de las veces anteriores que haya salido cara.
Es como jugar siempre al mismo número: ya tiene que quedar menos para que me toque. ¿Os suena?
Es probable que muchos de los apostantes ya conozcan esta teoría del instituto, pero que como eso no vale para nada, la hayan desterrado al rincón de las cosas aburridas.
A los que apostéis, siento deciros: no es prudente apostar sin conocer la teoría de la probabilidad. Económicamente, es la crónica de una muerte anunciada.
Bien vemos que es fácil comprobar que el pensamiento matemático estructurado corrige a nuestra intuición cuando esta se mete en terrenos que no le corresponden, y que es capaz de predecir hechos futuros, como, por ejemplo, el de hacia dónde previsiblemente va a moverse una cierta cantidad de dinero, para colocar allí discretamente nuestro bolsillo.
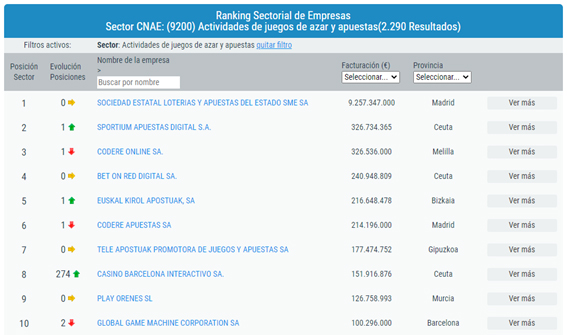
Pero comentamos una más. Nos queda hablar sobre su capacidad de abstracción.
Hasta ahora, aunque sin indicarlo tan expresamente, hemos hablado de cálculo y de estadística. De cómo obtener resultados concretos aplicables a situaciones bien definidas, tales como recoger el máximo de cubos sin cansarme innecesariamente, y de cómo obtener un dinerillo trileando a un grupo de personas. Estas vertientes forman parte de lo que se denomina matemática aplicada, que como su nombre indica, son aquellas que se pueden aplicar a problemas concretos para obtener resultados concretos. Son las matemáticas de los números.
¿Es que hay otras matemáticas que no se hacen con números? ¿Con qué se hacen, con bolas de anís?
Pues sí, hay matemáticas que se hacen sin números. Puede, de hecho, que ni aparezcan, y, de hacerlo, lo hacen para complementar el mensaje, de forma no estructural. Son las matemáticas abstractas. Las matemáticas de las letras.
Para finalizar, vamos a hablar de álgebra. Reconozco que, mi atracción por las matemáticas se debe a ella. No soy muy amigo del cálculo, aunque comprendo y agradezco sus aplicaciones, y, por supuesto, cuando veo que puede aportarme algo, lo uso.
Soy algo más amigo de la estadística, básica, o exclusivamente, mejor dicho, por su relevancia y potencia cuando se usa en conjunción con el software en la rama de la Inteligencia Artificial. Por lo demás, me parece una amiga un tanto traicionera. Con una mano te abraza, y con la otra te quita el bocata.
Pero el álgebra, amigos, es mi verdadero amor en cuanto a matemáticas se refiere.
Pero debo ser sincero. Esta última capacidad de las matemáticas que vamos a ver hoy (hay más, muchas más), puede no ser tan directamente aplicable como las anteriores.
Quiero con esto avisar, y por supuesto agradecer por haberlo hecho, a quienes hayan llegado hasta aquí.
No quiero echar a nadie, por favor, no me malinterpretéis, tan sólo quiero resaltar que, si bien todo saber es bueno, y una mente con capacidad de abstraerse es, casi siempre, un tesoro (tanto para uno mismo, como para su psicólogo, que básicamente vive de las consecuencias de ello), su aplicación no es tan directa. Viene bien, aporta mucho, pero lo hace de forma más general que aplicada, y, aunque es una de las claves para medrar profesionalmente, lo es más debido justo a esto, más a su enfoque generalista en cuanto a definir estrategias, que a su aplicación directa.
El álgebra no sólo aporta resultados. Aporta creaciones.
Si bien con el cálculo puedes aplicar complejas ecuaciones que te permitan saber cómo debes diseñar un puente para que este sea seguro, con el álgebra se descubren y se generan nuevas fórmulas de cálculo para hacerlo. Son, en esencia, la parte artística y creativa de las matemáticas.
Todo esto comienza con Al-Juarismi. O mejor dicho, con Abu Abdallah Mu?ammad ibn M?s? al-Jw?rizm?, un árabe nacido en el SVIII.
¿Árabes en ciencia y matemáticas?
Sí, amigos. Árabes. Y dadles casi todas las gracias. Las matemáticas que tenemos hoy en día son, esencia, suyas. Suyas, por difusión, ya que fueron una potencia cultural y científica desde nuestra baja edad media, hasta nuestro renacimiento, expandiendo su conocimiento desde oriente hasta Fisterra, para quien lo quisiese escuchar. Nosotros no quisimos.
Y suyas, también, por aportaciones, las cuales fueron enormes. Y este señor, es uno de los grandes. De hecho, se le considera el padre del álgebra 9.
Bien, pues este señor se planteó, como reto personal, encontrar la solución a todos los problemas. Así, para empezar. No pretendía tomar un problema concreto, como, por ejemplo, la cuadratura del círculo, y darle solución. Él opinaba, aún no sabemos sin con razón o sin ella, tal es la profundidad de este objetivo, que debía existir una secuencia de pasos que, aplicándola, permitiese identificar la forma de solucionar cada problema.
Fijaos en varias cosas.
Cada problema, sin importar cuál. Sin conocerlo de antemano. Ojo al manojo.
Secuencia de pasos. ¿Qué es una secuencia de pasos que, aplicándola, resuelve un problema? Un algoritmo.
¿Algoritmo? ¿Al-Juarismi? Mmmmmmm….
Si, ¿verdad? De ahí viene. Los que hacemos software se lo debemos todo. Él puso en marcha la idea de que se pueden tener ideas que generen formas de resolver problemas. Redefinió la dinámica en la que podemos abordar un problema. Ya no sólo está la forma clásica de [problema – solución al problema]. Ahora tenemos, también, [problema – generalización del problema – solución general que soluciona este y vete tú a saber cuántos subproblemas más].
Cuando somos capaces de pensar siguiendo la segunda pauta en lugar de la primera, decimos que nos estamos abstrayendo. Y, creedme, las soluciones que se alcanzan gracias al poder de la abstracción son BRUTALMENTE más potentes que las que se alcanzan con una solución aplicada, acoplada al dominio del problema.
Ni es fácil de usar, ni siempre ni todos podemos. Es una especie de meta-cognición, y eleva nuestras capacidades intelectuales a un nuevo nivel.
Veamos un ejemplo. Hay un algoritmo para multiplicar, y otro, para dividir. Todos los conocemos. Sabemos que, aplicando cierta secuencia de pasos, obtenemos el resultado correcto. No sabemos por qué, pero sabemos que sí. En la práctica, esto no importa. Pa’lante.
Pero si pensamos un poco, saliéndonos del ámbito de los números, vemos que ambas son dos operaciones que cumplen con las mismas propiedades (conmutativa, distributiva, etc.), y se aplican sobre un mismo conjunto que debe, también a su vez, cumplir otras (el conjunto de los números, el cual debe disponer de un elemento neutro, estar ordenado de forma lineal, etc.)
_____________________
9 Si recordáis, en el colegio siempre nos decían, dada nuestra fuerte historia árabe, que todo aquello que comience por ‘al’, casi seguro, es de origen árabe. Álgebra.
Pues si pensamos a este nivel, podemos llegar a deducir cuáles son las reglas de la multiplicación y la división. Es decir, sabremos, además del cómo, el porqué.
Pero es más. Si subimos aún más en el nivel de abstracción, podremos ver la naturaleza que subyace al concepto multiplicación-división, y aplicarlo a otros conjuntos. No se multiplican igual dos números que pertenecen al conjunto de los números naturales, infinito y ordenado linealmente, que a un retículo, también ordenado, pero no linealmente, y finito por naturaleza, con su supremo y su ínfimo.
Y si subimos más, veremos la naturaleza de las operaciones y los conjuntos en general. Así, hasta que, abstrayéndonos más y más, acabemos llegando a la cima, momento en que nos encontraremos ante el problema supremo, dado que habremos generalizado ya tanto los problemas específicos, que todos ellos han quedado enmarcados dentro de uno solo y general que los contiene a todos.
Esto es fácil de ver hasta este punto, pero llevarlo a cabo queda reservado a las capacidades de un pequeño puñado de personas a lo largo de toda la humanidad. Para el resto es difícil, por no decir imposible, seguir sin trabas estos razonamientos tan abstractos, pero poderosos.
Este buen hombre, obviamente, no acabó descubriendo el algoritmo que aplicándolo con un problema como variable (menuda variable), generase la secuencia de pasos necesaria para resolverlo.
Pero, por el camino, se dejó perlas tales como métodos de resolución de ecuaciones lineales y cuadráticas (los primeros métodos, de hecho), multitud de aportaciones a la trigonometría, etc.
¡Ah!, y de paso aportó toda una nueva técnica de razonamiento, y la fundamentó, regalándonos el álgebra, que casi se me olvida.
Vamos, es, sin duda, una piedra clave en el conocimiento humano.
La pregunta, en este caso, no es ¿para qué vale en la práctica? La pregunta, en este caso, es, ¿cuánto tiempo más seguirá siendo útil esta idea y esta herramienta? Es posible que lo sean para siempre.
A mi juicio, y creo que por motivos puramente culturales, religiosos, y políticos, no se otorga a este señor el peso que se merece en la historia de la humanidad en base a los aportes que nos dejó. No me malinterpretéis, en círculos científicos y matemáticos lo tiene. Me refiero a nivel social y popular.
No tiene sentido idolatrar a Edison, y olvidar a Al-Juarismi. El primero, no hubiese sido nadie sin el segundo, pero, obviamente, al revés no se cumple la misma afirmación.
Oye, no quiero molestar, pero, ¿tienes pensado acabar?
Sí, tenéis razón. Perdonad. Son temas apasionantes, y se me calienta la pluma. Ya terminamos.
Y para hacerlo, vamos a hablar sobre un último caso. Uno de los logros más importantes en esto de la matemática abstracta. Vamos a hablar del infinito. Y es que el infinito es al álgebra, lo que el cero es al cálculo. Parecen una obviedad y una nimiedad, tan sólo uno más de tantos, pero lo cierto es que tienen muchísima más enjundia, y su ausencia en nuestros modelos acarrearía tantos problemas, que básicamente los tumbaría. Se nos derrumbaría el castillo. Y como vamos a ver, jugar con el infinito no sólo es divertido (sí, sé que a estas alturas ya no me creéis), sino que no es tan obvio como a priori pueda parecer.

¿Es que acaso el infinito no es algo que nunca acaba? Sí, exacto. Pero tiene sus cosas. Funciona diferente. Veamos.
Por ejemplo, tenemos el concepto del tamaño. No todos los infinitos son iguales. Los hay mayores que otros.
¡Claro!, si a infinito le sumo uno, tengo infinito más uno, es mayor. Buen intento, pero no. Si a un infinito, le sumas algo, obtienes otro infinito del mismo tamaño.
¡Qué! ¡Eso no puede ser! ¡En el segundo infinito habrá un número más! No, de verdad, no es así. Pero no me creáis, vamos a razonarlo.
Para ello, tenemos que partir de lo siguiente: un infinito es un conjunto sin fin. Esto puede parecer obvio, pero si a un conjunto sin fin, le añado un elemento, vuelvo a tener lo mismo: un conjunto sin fin.
Para que un infinito sea mayor que otro, debe serlo su conjunto, no su cardinal (que no existe). Es decir, un infinito no puede crecer. El infinito no se alcanza, infinito se es. No podemos, partiendo de un conjunto finito, añadir elementos hasta alcanzar el infinito, ya que nunca pararíamos de añadir elementos, pero obteniendo con ello, de nuevo, otro conjunto igualmente finito, aunque, ahora sí, mayor.
Para esto, hemos de separar los conceptos de infinito, y los de contar hasta el infinito. El primero está asociado a un conjunto. Concretamente a uno no vacío, y que no tenga un número finito de elementos. Lo segundo, es imposible, ya que, aunque contemos durante eones, nunca alcanzaremos una frontera en la que pasemos de algún número muy grande, al infinito. Siempre obtendremos otro número finito, no importa el tiempo que nos mantengamos contando.
Tomemos el conjunto de los números naturales. Los de siempre, los de toda la vida: 1, 2, 3, 4, 5, etc.) Este conjunto no contiene una cantidad concreta de elementos, es infinito.
Tomemos ahora el conjunto de los números naturales pares. También conocido, nada raro: el 2, el 4, el 6, etc. Coincidiremos en que este conjunto es, también, infinito.
Bien, pues, ¿cuál es mayor? El primero. Tiene el doble de elementos, está claro. Ahora entiendo a qué te referías con eso de infinitos de diferentes tamaños…
Pues, siento decirlo, pero no. De nuevo la intuición dando malos consejos... ¿Qué no? ¡De esta no me sacas, fijo que no!
Tranquilos, razonemos. Como Gauss, y esta vez, además de una forma muy muy parecida a como él lo hizo.
Ambos conjuntos son igual de grandes, es decir, el tamaño de su infinito es igual, debido a que puedo emparejar todos sus elementos, uno a uno, sin que en ninguno de ellos queden elementos sueltos. En este caso, claramente, puedo emparejar el 1 con el 2, el 2 con el 4, el 3 con el 6, y así sucesivamente, de tal forma que no deje nunca elementos libres en ninguno de los conjuntos.
Nuestra intuición nos dirá que habrá elementos del conjunto de todos los números naturales que se queden libres cuando se gasten los pares, pero es que, recordad, no se gastarán. Es un conjunto infinito. Siempre habrá un par para un natural. Siempre. Por eso indicaba antes que el infinito no se alcanza, infinito se es. Desde el principio. Se nace infinito. Como el que nace guapo. Si no naces guapo, da igual lo que te añadas. Siempre serás un feo con cosas, pero nunca alcanzarás la guapura.
Mira, hoy me tienes hasta las narices. Haber empezado por ahí, resulta entonces que todos los infinitos son iguales. En dos conjuntos infinitos, siempre habrá una pareja para cada elemento, dado que en ambos conjuntos hay infinitos. Cada día me caes peor..
Reconozco lo de hoy, es demasiado, tanto en extensión, como en giros de guion. Pero no es retranca. Realmente no hay trucos. Parece que hay truco porque, una vez más, asumimos como válida la respuesta inmediata de la intuición, pero cuando la razonamos, vemos que no es correcta. Este sí pero no, es lo que os da la sensación de que os estoy tocando las narices. Pero no lo estoy haciendo, de verdad.
Tomemos esta vez otro conjunto. El de los números reales. Para no perder tiempo: el de todos los números, incluyendo los decimales. Pues en este conjunto, resulta que el subconjunto que hay entre 0 y 1, es infinito. Es obvio. Y es un infinito mayor que el de los números naturales o el de los naturales pares.
No oigo quejas, qué raro… ¿Qué debemos hacer para comprobarlo? Efectivamente: razonar.
Con el subconjunto [0-1] de los números reales, no puedo ni comenzar a emparejar, ahí está la clave. Antes, tomábamos el primer elemento de un conjunto, y le asignábamos el de la misma posición del otro, y así sucesivamente. Pero, ¿cuál es el primer elemento aquí? Si digo que es 0.1, me diréis que no, que es 0.01. Y al aceptarlo, me diréis que no, que coja 0.001. Y cuando os lo acepte de nuevo, me diréis que no, que coja 0.0001. Y así infinitas veces.
Por tanto, si bien el conjunto de los números naturales tiene infinitos elementos, el conjunto de los números reales no sólo tiene a estos, sino la capacidad de seguir generando elementos de forma infinita. Si los emparejo dos a dos, es fácil ver (ejem, ejem) que me sobrarán elementos en el segundo. Por tanto, los conjuntos de los números naturales y el de los reales son ambos infinitos, pero el segundo es mayor. Su infinito es más grande. Y además es un infinito incontable. Esto es, siempre habrá elementos que, perteneciendo por definición al conjunto, no estén todavía en él. Estén sin generar. Aún no hayan nacido. Siempre podré sacar otro conejo de esa chistera
A todo esto se dedicó Georg Cantor, un matemático ruso del SXIX (murió ya en el SXX). Dedicó casi toda su vida profesional activa al estudio de los infinitos, obteniendo razonamientos como los que hemos utilizado arriba para jugar. Una vida de abstracto y sesudo pensamiento, que dejó unas aportaciones matemáticas sin las cuales buena parte de la física e ingeniería modernas no hubiesen podido desarrollarse.
El hombre acabó con sus huesos en un psiquiátrico. No os sorprende, ¿verdad?
Bien, suficiente por hoy. Podemos ir en paz.
¡¡¡¡¡¡¡Gracias!!!!!!!
Sí, os entiendo. Tenéis razón. Os agradezco inmensamente vuestro interés y tesón a los que hayáis llegado hasta aquí. La exposición, que no el tema, no son dignos del premio al relato más entretenido, lo he hecho lo mejor que he podido.
En serio: gracias.
Una vez más, esto es sólo una aproximación. Disculpen las carencias, disculpen, sobre todo, las licencias (pocas en esta ocasión), y sean benévolos con los errores que hayamos podido cometer. Como siempre, nuestra intención es entretener, y a poder ser, generar curiosidad y respeto por la Ciencia. Y con conseguir sólo una pizca de tan sólo una de ellas, sentiremos que nuestro trabajo ha merecido, sobradamente, la pena.
Y recuerda: ¡las matemáticas son tus amigas!
¡Nos vemos!

Entusiasta del software, la música, y la ciencia, llevo desde chaval metido en los tres tinglados todo lo que mi tiempo y mis capacidades me permiten. Estudié Ingeniería Técnica Informática en la Universidad de Castilla – La Mancha, Máster Universitario en Tecnologías Informáticas Avanzadas en la misma universidad, y Máster Universitario en Inteligencia Artificial por la Universidad Internacional de la Rioja, y me he dedicado al software durante toda mi vida profesional, así como a leer toda la divulgación posible sobre ciencia, especialmente en las ramas de la astrofísica y astronomía
<